[책] 통계 101 x 데이터 분석 요약 , 통계 개괄 스터디
by darami이 글은 책 '통계 101 x 데이터 분석 , 아베 마사토 저, 프리렉' 을 데이터 분석가 입장에서 요약하고 정리/변형한 글입니다. 🙏🏻
* 왼쪽 최상단 사이드바를 누르시면 글의 목차, 이동 기능을 이용하실 수 있습니다.
예상 독자
- 통계학의 전체적 흐름을 훑고 싶으신 분
- 많이 들어본 이름들이지만 정확히 어떤 의미인지 대략적인 정의를 알고 싶으신 분
- 현업에서 어떻게 통계를 사용할 지 인사이트를 얻고 싶은 분
- 이 책을 읽고 다시 공부할 글쓴이 자신 (유력)
1장. 통계학이란?
데이터 분석의 목적
1) 데이터를 요약하는 것
2) 대상을 설명하는 것
3) 새로 얻을 데이터를 예측하는 것
통계학의 전체 모습
1) 기술 통계 : 수집한 데이터를 정리하고 요약
2) 추론 통계 : 수집한 데이터로부터 데이터의 발생원을 추정
(1) 통계적 추론 방법 : 데이터에서 가정한 확률 모형의 성질을 추정하는 방법
(2) 가설검정 방법 : 세운 가설과 얻은 데이터가 얼마나 들어맞는지 평가, 가설을 채택할 것인가를 판단하는 방법
2장. 모집단과 표본
모집단의 크기 : 모집단에 포함된 요소의 수
- 유한 모집단
- 모집단 중 한정된 요소만 포함하는 것
- 예시 : 2020년 기준 한국인 약 5000만명
- 모집단 중 한정된 요소만 포함하는 것
- 무한 모집단
- 모집단 중 포함된 요소가 무한한 것
- 예시 : 신약 효과의 예, 미래에 고혈압으로 약을 복용할 사람도 포함되기 때문에 요소는 무제한
- 모집단 중 포함된 요소가 무한한 것
모집단의 성질
- 전수 조사
- 모집단의 성질을 아는 유일한 방법
- 모집단에 포함된 모든 요소를 조사하는 것
- 유한 모집단일 때 선택할 수 있음
- 데이터 분석 방법 : 기술 통계
- 획득한 데이터의 특징을 기술하고 요약하는 것만으로 모집단의 성질을 설명하고 이해할 수 있음
- 어려움 : 하지만 전수 조사에는 보통 막대한 비용이 들어감으로 어려움
- 표본 조사
- 모집단의 일부를 분석하여 모집단 전체의 성질을 추정하는 방법
- 전수 조사의 어려움으로 인해 필요해짐
- 표본(sample) : 추론통계에서 조사하는 모집단의 일부
- 표본추출(sampling) : 모집단에서 표본을 뽑는 것
- 표본의 크기와 표본의 수
- 표본의 크기 : 표본에 포함된 요소의 개수
- 보통 n으로 나타냄 (n=30)
- 예시 : 표본으로 30개 추출
- 표본의 개수 = 샘플 수
- 20명으로 이루어진 표본 A, 30명으로 이루어진 표본 B -> 샘플 수 2개
- 표본의 크기 : 표본에 포함된 요소의 개수
- 모집단의 일부를 분석하여 모집단 전체의 성질을 추정하는 방법
3장. 통계분석의 기초
데이터의 유형
변수
- 공통의 측정 방법으로 얻은 같은 성질의 값
- 변수의 개수는 '차원'이라고 표현되기도 함
- 양적 변수 (수치형 변수)
- 숫자로 나타낼 수 있는 변수
- 이산형
- 연속형
- 숫자로 나타낼 수 있는 변수
- 질적 변수 (범주형 변수)
- 양적 변수 (수치형 변수)
통계량
- 대푯값 (representative value)
- 대략적인 분포의 위치
- 평균값 (mean)
- 표본평균 등
- 중앙값 (median)
- 크기 순으로 값을 정렬했을 때 한가운데 위치한 값
- 수치 자체의 정보가 아닌 순서에만 주목하기 때문에 아웃라이어의 영향을 받지 않는다는 특징이 있음
- 최빈값 (mode)
- 데이터 중 가장 자주 나타나는 값
- 좌우 대칭이 봉우리 형태 라면 평균값, 중앙값, 최빈값은 대체로 일치
- 좌우 비대칭이라면 일치하지 않음
- 평균값 (mean)
- 한계
- 대푯값만으로 데이터를 이해하는 것은 경계해야 함
- 예시) 분포가 봉우리 형태가 아인 경우, 평균값을 계산하면 실제 데이터에서 멀리 동떨어진 값을 얻을 수 있음
- 때문에 히스토그램을 그려 대략적인 데이터 파악 후 데이터 분석을 해야 함
- 대푯값만으로 데이터를 이해하는 것은 경계해야 함
- 대략적인 분포의 위치
- 분산과 표준편차
- '데이터의 퍼짐'을 평가
- 분산(variance)
- 표준편차(standard deviation, S.D.)
- 표본에서 구한다는 점 강조
- 표본분산 (sample variance)
- 표본의 각 값과 표본평균이 어느 정도 떨어져 있는지를 평가함
- 각 값과 평균값 사이 거리의 제곱을 평균화한 값으로 데이터의 퍼짐 정도를 평가함
- 모든 값이 같다면 0
- 데이터 퍼짐 정도가 크면 s^2이 커짐
- 표본표준편차(sample standard deviation)
- s, 표본 분산의 제곱근을 취한 값
- 원래 값 단위와 일치하여 감각적으로 알기 더 쉽게 느껴짐
- 표본분산 (sample variance)
- '데이터의 퍼짐'을 평가
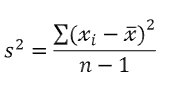
- 이상값
- 평균값에서 표준편차의 2배 또는 3배 이상 벗어난 숫자를 보통 이상값으로 봄
- 표준화 (standardizing, normalizing)
- 평균과의 거리가 표준편차의 몇 배인가를 나타냄
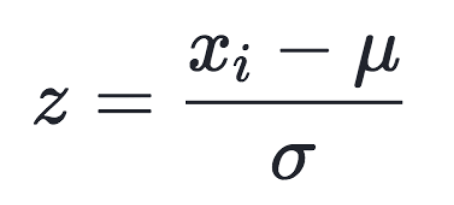
- 왜도와 첨도
- 기댓값과 분산 이외에도 확률분포를 특징짓는 값
- 왜도(skewness)
- 분포가 좌우대칭에서 어느 정도 벗어났는지
- 첨도(kurtosis)
- 분포가 얼마나 뾰족한지, 그래프의 꼬리가 차지하는 비율
- 왜도(skewness)
- 기댓값과 분산 이외에도 확률분포를 특징짓는 값
4장. 추론통계~신뢰구간
데이터를 얻는다는 것
- 무작위추출(random sampling)
- 단순무작위추출법
- 난수를 이용하여 표본을 정함, 노력과 시간 비용이 들 때가 있음
- 층화추출법
- 실제로 자주 사용함
- 모집단을 몇 개의 층으로 미리 나눈 뒤, 각 층에서 필요한 수의 조사 대상을 무작위로 추출하는 법
- 그 외
- 계통추출법, 군집추출법 등
- 단순무작위추출법
- 정말로 알고 싶은 것 : 모집단
표본오차와 신뢰구간
- 표본오차(sampling error)
- 추정량
- 모집단의 성질을 추정하는 데 사용하는 통계량
- 신뢰구간
- oo% 신뢰구간 mean "oo%의 확률로 이 구간에 모집단평균 u가 있다.
- t 분포
- 표본크기 n이 작아도 적용 가능하려면, '정규분표에서 얻은 데이터'라는 가정이 필요함
- 표본 크기 n이 이 크면 clt에 따라서 모집단이 정규분포가 아니더라도 표본평균을 정규분포로 근사할 수 있음으로 신뢰구간은 정확해짐
- t 분포
- oo% 신뢰구간 mean "oo%의 확률로 이 구간에 모집단평균 u가 있다.
5장. 가설검정
가설검정의 원리
- 가설 검정
- 실험군(treatment group)
- 대조군(control group)
- p값
- 귀무가설이 옳다고 가정했을 때 관찰한 값 이상으로 극단적인 값이 나올 확률
- p값이 0.05 이하인 경우, 귀무가설 하에서 현실 데이터는 나타나기 어렵다고 생각하고 귀무가설을 기각, 대립가설을 채택
- 통계적으로 유의미한 차이가 있다. 제1종 오류와 제2종 오류
- 제1종 오류
- 귀무가설이 옳으나 귀무가설 기각, false positive
- 제1종 오류가 일어날 확률 : a
- 예시) 실제로는 아무런 차이가 없음에도 차이가 있다고 판단해 버리는 잘못
- 유의 수준 a의 값을 미리 정해둠으로 확률을 통제할 수 있음
- 제2종 오류
- 대립가설이 옳음에도 귀무가설을 기각하지 않음, false negative
- 제2종 오류가 일어날 확률 : B
- 제2종 오류가 일어나지 않는 확률 (차이가 있을 때 차이가 있다고 올바르게 판단할 확률) : 검정력
- 1-B
- 일반적으로 80%로 설정
- B는 a와 달리 직접 통제할 수 없음
- 1-B
- 제2종 오류가 일어나지 않는 확률 (차이가 있을 때 차이가 있다고 올바르게 판단할 확률) : 검정력
- a와 B는 상충관계에 있음
- 7장. 상관과 회귀
상관관계
- 피어슨 상관계수
- -1 ~ +1까지의 실수값
- 주의할 점
- 상관계수 r은 2개 양적 변수의 선형 관계성 강도를 정량화한 것, 비선형 관계는 r로 적절하게 정량화할 수 없음
- r은 강도를 정량화하기에, 직선의 기울기 크기는 관계가 없다.
- 데이터로 상관계수를 계산하기 전에 산점도를 그려 데이터가 어떻게 분포하는지를 미리 확인해야 함
- 상관계수가 같은 데이터는 비선형을 포함해 다양한 형태가 있음으로
- r은 평균이나 분산에 기반한 모수적인 방법, x나 y의 분포 모두 정규 분포라고 가정
- 이상값이 있을 때는 적절하지 않음
- 정규성을 샤피로-윌크 검정 등으로 확인한 후 정규성이 한쪽에 조금이라도 없다면 비모수 상관계수를 이용하는 것이 좋음
- 이상값이 있을 때는 적절하지 않음
- 비모수 상관계수
- 데이터의 x축, y축 중 적어도 하나 이상에 정규성이 없을 때, 비모수 상관계수인 스피어만 순위 상관계수가 권장
- -1 ~ +1까지의 실수값
- 이상값이 있을 때도 사용할 수 있음
- 주의할 점
- 상관관계 계산 시 2개 변수가 처음부터 종속 관계이면 주의가 필요
- x와 y축의 값이 개별 변수일 것, 그리고 나눗셈 등으로 변환하지 않았을 것을 사전에 확인
- 상관관계 계산 시 2개 변수가 처음부터 종속 관계이면 주의가 필요
선형회귀
상관과 달리 회귀에는 설명변수 x와 반응변수 y라는 비대칭성이 있음
- 단순 회귀의 예시
- f(x)가 1차 함수, y= a + bx
- f(x)의 형태를 결정하는 파라미터 a,b를 회귀계수 (regression coefficient)라고 함
- f(x)가 1차 함수, y= a + bx
회귀모형 (regression model)
y = a + bx + 𝜖
- 𝜖 : 모집단에 대한 확률 오차
- x : 설명변수
- y : 설명변수 x에 대한 반응변수의 실현값
- 최소제곱법 (least squares)
- a 와 b를 정하기 위해서 모형의 '좋음'을 판단하는 기준이 있어야 함
- 데이터에 가능한 한 들어맞는 회귀모형이 좋은 모형이라고 생각할 수 있음
- 가능한 한 들어맞는 : '데이터와 회귀식의 차이가 가능한 한 작은' 이 될 수 있음
- 데이터에 가능한 한 들어맞는 회귀모형이 좋은 모형이라고 생각할 수 있음
- 데이터와 모형 차이의 제곱을 모두 더한 값 E를 최소화하는 방법
- a 와 b를 정하기 위해서 모형의 '좋음'을 판단하는 기준이 있어야 함
8장. 통계 모형화
선형회귀 원리의 확장
실제 데이터 해석에서는 설명변수가 여러개인 경우, 반응변수가 양적 변수가 아니라 예/아니요 같은 범주형 변수일 때도 있음으로 회귀 모형이 항상 적절하지는 않음
- 확장 방향성
- 설명변수의 개수를 늘리거나 유형 변경하기
- 반응변수의 유형 변경하기
- 회귀모형의 형태 변경하기
- 다중회귀
- 설명변수가 여러 개인 것
- 단순 회귀 : 설명 변수가 1개인 것
고차원 데이터 문제
- 차원의 저주
- 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가함
- 차원이 증가할수록 다중공선성 문제가 일어나기 쉬우며 추정 정밀도가 떨어짐
- 차원 축소 등의 방법이 있음
- 차원이 증가할수록 다중공선성 문제가 일어나기 쉬우며 추정 정밀도가 떨어짐
- 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가함
- 다중공선성
- 설명변수가 여러 개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우
- 회귀 계수의 추정오차가 커지는 문제가 발생할 가능성이 있음
- 추정값의 신뢰성이 떨어짐
- 다중공선성이 강할 때
- 서로 상관이 있는 2개 변수 중 하나를 없앰
- 주성분분석 등의 차원 축소 방법을 이용하여 설명변수의 개수를 줄임
- 설명변수가 여러 개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우
- 푸아송 회귀
- 데이터가 음수가 되지 않는 정수일 때, 특히 반응변수가 개수인 경우 고려해 볼 수 있는 일반화선형모형 9장. 가설검정의 주의점
9장. 가설검정의 주의점
가설 검정의 이치를 제대로 이해하지 않아도, '선행 연구를 모방하여 가설 검정을 시행, P <0.05를 얻기만 하면 그만'이라 여기는 사용자가 많다는 것이 실정
이러한 실정으로 인해 재현성의 위기가 일어남
재현성
- 재현성 위기
- 과학에서의 재현성(reproducibility, replication)
- 누가 언제 어디서 실험하더라도, 조건이 동일하다면 동일한 결과를 얻을 수 있어야 한다는 것
- 예시) 신약 효과나 부작용 조사 실험의 재현성
- 누가 언제 어디서 실험하더라도, 조건이 동일하다면 동일한 결과를 얻을 수 있어야 한다는 것
- 최근 논문으로 발표된 내용을 다른 연구자가 동일한 방법과 조건으로 추시했을 때 같은 결과를 얻지 못하고 있다는 보고가 잇따르고 있음
- 과학에서의 재현성(reproducibility, replication)
- 재현 불가능한 원인 (낮은 재현성)
- 실험 조건을 동일하게 조성하기 어려움
- 가설검정의 사용 방법을 조작할 수 있음
- p-해킹 (p-hacking)
- 의도치 않게 저지를 수 있음
- p-해킹 (p-hacking)
가설검정의 문제점
- p값의 정의
- '귀무가설이 옳다고 가정할 때 실제 관찰한 데이터 이상으로 극단적인 값을 얻을 확률'
- 이 값이 작으면 귀무가설과 관찰한 데이터 사이에 괴리가 크다는 것을 의미, 유의 수준 a를 밑도는 때에는 귀무사설을 기각
- '귀무가설이 옳다고 가정할 때 실제 관찰한 데이터 이상으로 극단적인 값을 얻을 확률'
- 왜 a=0.05를 사용하는가?
- 딱히 근거는 없음, 관례처럼 사용됨
- 때문에 귀무가설이 옳은데 기각할 가능성을 줄이기 위해서 a를 더 줄일 수 있지만 그러면 B가 커져 버리는 문제가 있음
- 딱히 근거는 없음, 관례처럼 사용됨
- 피셔류 검정과 네이만-피어슨류 검정
- 피셔류 검정
- 귀무가설이 옳을 때 관찰한 데이터 이상으로 극단적인 값을 얻을 확률인 p값을 계산
- 귀무가설과 관찰한 값의 괴리 정도를 평가
- 가설을 기각한다는 개념 X , p값의 크기에 따라 증거의 강력함을 평가
- 네이만-피어슨류 검정
- 대립가설 설정, 제1종 오류, 제2종 오류를 고려하는 현대 가설검증의 흐름을 만듦
- p값이 유의 수준 a 미만인가 이상인가에만 주목, 가설 기각/채택이라는 결론 내림
- 미리 검출하고자 하는 효과크기를 정하고, 설정한 a와 B에 따라 필요한 표본크기 n을 결정해야 함
- 표본크기 n이 크면 아주 약간의 차이라도 귀무가설을 기각하기 때문
- 실제 현대 가설 검정에서는 p감ㅅ이 0.05보다 큰지 작은지가 아닌, p 값 자체를 기재하거나 * 기호룰 붙일 것을 권장
- 피셔류 검정
효과크기
- 효과크기(effect size)
- p값으로 귀무가설이 옳다고 생각하기 어렵고, 평균값에 얼마나 차이가 있는지 말해주지 않음
- 얼마만큼의 효과가 있는지를 나태는 것
- Cohen's d
- 2개의 모집단평균이 얼마나 떨어져 있는지를 나타냄
- 상관계수, 결정계수 등 다양한 효과크기 적용 가능
- p값과 함께 검정 방법에 따라 다양한 효과 크기를 함께 나타내는 것이 주류
- Cohen's d
베이즈 인수
- 베이즈 인수의 특징과 주의점
- p값 문제에서 귀무가설과 대립가설 간 비대칭성 문제는 베이즈 인수에 해당하지 않음
- 두 가설의 상대적인 비교일 뿐, 사후 예측 점검을 수행할 필요가 있음
- 파라미터의 사전분포에 영향을 받음
- 주변 가능도를 구할 때는 모형으로 설정한 파라미터로 평균화하기 위한 적분 계산이 필요함
p-해킹
- p-해킹
- 의도하든 의도하지 않든, p값을 원하는 방향으로 조작하는 행위
- 수치 고치는 것 x , p값이 0.05 미만이 되도록 실험을 설계하거나 해석하는 것
- 재현성의 저하로 이어짐
- 결과를 보며 표본크기(n)를 늘려서는 안 됨
- 마음에 드는 해석만 보고해서는 안 됨
- HARking
- 'Hypothesis After the Results are Known'의 약자
- 데이터를 얻어 결과를 보고 나서 가설을 만드는 행위
- 재현성의 저하로 이어짐
- HARking
- p-해킹을 예방하기 위한 노력들
- 가설검증형 연구와 탐색형 연구
- 가설검증형 연구
- 가설을 세우고 이를 검증하는 연구
- 이 연구에 따라 올바르게 가설검증을 사용하는 것이 이상적
- 가설을 세우고 이를 검증하는 연구
- 탐색형 연구
- 전체를 탐색적으로 해석하는 연구
- 탐색형 연구밖에 할 수 없는 상황이라면 실험이나 해석에 사용한 변수를 모두 보고, 검정을 반복한 횟수로 유의 수준 a를 나누는 본페로니 교정으로 이를 보정해야 함
- 검정의 다중성을 놓치기 쉬움
- 사전 등록
- 연구를 실시하기 전에 가설과 실험 설계, 분석 방법 등의 연구 계획을 등록하는 것
- 등록한 내용에 따라 연구를 진행함으로 데이터를 얻은 다음 가설을 세우는 HARKing을 막을 수 있음
- p값 관련 문제 정리
- p값을 제대로 이해하고 사용한다
- 전체를 탐색적으로 해석하는 연구
- 가설검증을 반복하면 다중성 문제가 발생하고, 위양성이 증가한다는 것을 이해한다.
- 탐색형 연구와 가설검증형 연구의 차이를 이해한다.
- 실시한 실험이나 해석은 제대로 보고한다.
- 재현성이 있는지 염두에 둔다. 가능하다면 재실험하여 확인한다.
- 좋은 가설을 세운다.
- 가설검증형 연구
- 가설검증형 연구와 탐색형 연구
10장. 인과와 상관
인과관계와 상관관계
- 인과관계
- 원인과 결과의 관계
- 원인 -> 결과라는 방향성이 특징
- 원인과 결과의 관계
- 상관관계
- 데이터에서 보이는 관련성 (association)
- 일반적, 어떤 특정한 조합이 일어나기 쉽다
- 수학적, 확률변수 사이가 독립이 아니라는 뜻
- 상관계수는 두 양적 데이터의 관련성을 수치화한 것, 상관관계는 데이터 유형을 따르지 않는 넓은 개념
- 데이터에서 보이는 관련성 (association)
- 인과와 상관의 차이
- 중첩요인(중첩변수, confounder)
- 두 변수에 관련된 외부변수가 존재할 때, 이를 중첩이라 하고, 그 변수를 중첩변수/요인이라고 함
- 예시) 아침밥과 성적의 관계에 제3의 변수인 가정환경이라는 요인이 있을 수 있다.
- 이러한 중첩 요인 데이터도 수집해 분석에 사용하는 것이 중요하다.
- 중첩요인을 고려함으로써, 알고자 하는 변수의 인과효과크기를 평가할 수 있다.
- 두 변수에 관련된 외부변수가 존재할 때, 이를 중첩이라 하고, 그 변수를 중첩변수/요인이라고 함
- 중첩요인(중첩변수, confounder)
- 인과-상관-허위상관
- 허위상관(spurious correlation)
- 인과관계는 없지만 상관관계는 있을 때, 인과관계가 있는 것처럼 보이는 상관이라는 뜻
- 인과관계가 있어도 상관관계가 없을 수 있음
- 중첩요인 or 합류점 편향이 있을 때
- X -> Y -> Z 라는 중간 변수가 있을 때
- 선형이 아닌 상관일 때
- 허위상관(spurious correlation)
- 인과관계를 알면 할 수 있는 일
- '개입'이 가능해짐
- 원인 변수를 변화시킴으로써(개입) , 결과 변수를 바꿀 수 있음
- '개입'이 가능해짐
- 상관관계를 알면 할 수 있는 일
- 한쪽 변수로부터 또 다른 변수를 '예측'할 수 있음
인과관계와 상관관계의 다양한 사례
- 시간과 나이는 중첩요인이 되기 쉬움
- 우연히 생긴 상관
- 수많은 변수를 마구잡이로 해석하면 통계적으로 유의미한 결과를 얻을 수도 있다는 문제
- p-해킹 이나 HARKing과 비슷함
무작위 통제 실험
- 무작위 통제 실험 (randomized control trial , RCT)
- 변수 X에서 변수 Y로의 인과효과를 추정하는 가장 강력한 방법
- 알고자 하는 요인인 변수 X에 표본을 무작위로 할당하고 개입 실험을 수행한 다음, 변수 Y와 비교하는 방법
- 비즈니스 분야에서는 'AB 테스트'라고 부름
- 왜 인과효과를 추정하는 강력한 방법일까
- 중첩요인을 확인하지 않더라도, 그 효과를 무작위를 이용하여 무효화할 수 있으므로, 알고자 하는 변수의 효과만 추정 가능
- 변수 X에서 변수 Y로의 인과효과를 추정하는 가장 강력한 방법
- 통계학에서의 인과관계
- 2개의 변수 X와 Y가 있을 때 아래와 같다면
- X=0 , 글쓴이가 영양제를 3개월간 먹지 않음 (개입 없음)
- Y(0) :글쓴이가 영양제를 3개월간 먹지 않았을 때의 건강 상태
- X=1 , 글쓴이가 영양제를 3개월간 먹음 (개입 있음)
- Y(1) : 글쓴이가 영양제를 3개월간 먹었을 때의 건강 상태
- t (인과효과, 개입 효과) = Y(1)-Y(0)
- 글쓴이가 영양제를 3개월간 먹었을 때의 건강 상태 -글쓴이가 영양제를 3개월간 먹지 않았을 때의 건강 상태
- 현실에서는 개인의 세계 양쪽을 관찰할 수 없기 때문에 이것은 불가능함
- --> 인과추론의 근본 문제
- X=0 , 글쓴이가 영양제를 3개월간 먹지 않음 (개입 없음)
- 무작위 통제 실험의 이론적 배경
- 개인 수준이 아닌 집단 수준을 생각하여 인과의 평균적인 효과를 고려할 수 있음
- t (인과의 평균적인 효과)= E[ Y(1) - Y(0) ] = E[Y(1)] - E[Y(O)]
- E[ ] : 모집단의 기댓값
- 이 경우에도 영양제를 먹었을 때와 안 먹었을 때 두 개 모두를 관찰할 수 없고, 영양제를 먹는 집단에 할당된 사람의 건강 상태와 영양제를 안 먹는 집단에 할당된 사람의 건강 상태 간 기댓값 차이를 알 수 밖에 없음.
- 때문에 여러 과정을 거쳐 피험자를 무작위 할당하고, 반년 후 t 검정 등으로 건강 상태를 비교하면 인과 효과를 비교할 수 있음
- 선택 편향
- 중첩요인의 존재가 선택편향을 발생시켰기 때문에 인과관계를 밝혀 내기가 어려웠음
- 무작위 할당이 아닌 경우에, 영양제를 먹는 사람과 영양제를 안먹는 사람에서 잠재적인 건강 상태의 차이를 발견할 수 있음
- 예시) 애초에 영양제를 꾸준히 먹는 사람들은 건강 상태 증진에 대한 의욕적이라고 할 수 있음
- 무작위 할당이 아닌 경우에, 영양제를 먹는 사람과 영양제를 안먹는 사람에서 잠재적인 건강 상태의 차이를 발견할 수 있음
- 중첩요인의 존재가 선택편향을 발생시켰기 때문에 인과관계를 밝혀 내기가 어려웠음
- 2개의 변수 X와 Y가 있을 때 아래와 같다면
통계적 인과 추론
무작위 통제 실험이 어려울 때, 통계적 인과 추론을 사용함
- 다중회귀
- 중첩요인을 측정해 모형에 도입하는 것이 중요
- 조정 : 중첩 요인을 포함
- 인과 그래프를 그리고, backdoor기준에 따라 모형 투입 여부를 결정하는 것이 바람직함
- 층별 해석
- 중첩요인을 기준으로 데이터를 몇 가지 그룹(층)으로 나누어, 각 층 안에서 중첩요인의 효과를 가능한 한 작게 하는 법
- 경향 점수 짝짓기
- 짝짓기(matching)
- 원인변수=0 인 집단과 원인변수=1인 집단에서 비슷한 중첩요인을 가진 데이터를 골라 쌍으로 만드는 방법
- 중첩요인 값이 비슷한 데이터를 짝지으면 중첩요인 효과를 없애고 무작위 통제 실험과 비슷한 효과를 얻을 수 있음
- 경향 점수 짝짓기(Propensity Score Matching, PSM)
- 경향 점수라는 1차원 값을 기준으로 쌍을 고르는 방법으로 자수 사용됨
- 순서
- 반응 변수를 원인 변수 (0 또는 1)로 하고, 중첩 요인을 설명변수로 한 로지스틱 회귀를 실행
- 이에 따라 어떤 중첩 요인을 원인변수=1에 할당할 것인가를 평가
- 고른 쌍으로 반응변수의 차이를 계산, 그 평균값을 취해 효과 추정량으로 삼음
- 경향 점수 짝짓기(Propensity Score Matching, PSM)
- 중첩요인 값이 비슷한 데이터를 짝지으면 중첩요인 효과를 없애고 무작위 통제 실험과 비슷한 효과를 얻을 수 있음
- 원인변수=0 인 집단과 원인변수=1인 집단에서 비슷한 중첩요인을 가진 데이터를 골라 쌍으로 만드는 방법
- 짝짓기(matching)
- 이중차분법 (Difference In Differences, DID)
- 시간 축을 도입, 집단 간 차이에 대해 다시 한번 처리 전후의 차분을 취함으로써 인과효과를 추정
11장. 베이즈 통계
베이즈 통계의 사고방식
- 통계학의 2가지 흐름
- 빈도주의 통계
- 지금까지 다룬 다양한 통계 방법
- 베이즈 통계
- 조금 다른 사고방식에 기초, 중요성이 더욱 커질 것으로 보임 (컴퓨팅)
- 빈도주의 통계
- 불확실성 다루기
- 빈도주의에서
- 불확실성
- 모집단에서 표본을 추출할 때의 불확실성
- 확률
- 무한히 반복 실행한 결과로써의 객관적인 빈도를 나타냄
- 불확실성
- 베이즈 통계에서
- 불확실성
- 모집단 분포 모형화 : 분석자가 파라미터 𝜃를 어느 정도 알고 있는지를 확률 분포로 나타냄
- 데이터 x를 얻어 𝜃에 대한 정보를 알아내면, 𝜃의 불확실성이 줄어둘고 𝜃의 확률 분포가 달라지는 모습을 보임
- 확률
- '얼마나 확신하는지'로 해석하는 원리 베이즈 통계의 사고방식
- 불확실성
- 빈도주의에서
- 베이즈 통계의 사고방식
- 베이즈 통계에서는 통계 모형의 파라미터 𝜃를 확률변수로 취급하여, 그 확률 분포를 생각함
- 사전분포 p(𝜃)를 마련해 두고, 이를 이용하여 사후분포 p(𝜃lx)를 구하는 것이 베이즈 통계에서의 추정
- 사전분포 p(𝜃) (prior distribution)
- 분석자가 데이터를 알기 전 단계의 𝜃 확률 분포
- 사후분포 p(𝜃lx) (posterior distribution)
- 사전분포를 이용하여 데이터를 안 후의 파라미터 𝜃의 확률분포
- 사전분포 p(𝜃) (prior distribution)
- 사전분포 p(𝜃)를 마련해 두고, 이를 이용하여 사후분포 p(𝜃lx)를 구하는 것이 베이즈 통계에서의 추정
- 베이즈 통계에서는 통계 모형의 파라미터 𝜃를 확률변수로 취급하여, 그 확률 분포를 생각함
베이즈 통계 알고리즘
- MCMC (Markov Chain Monte Carlo method) 방법
- 사후분포를 직접 계산하기 어렵기 때문에 사용하는 계산 알고리즘
- 특정 확률분포를 따르는 난수 발생 알고리즘
- 베이즈 통계에서는 이것을 이용하여 사후분포를 따르는 난수를 발생시키고, 난수의 집합을 관찰함으로써 사후분포의 성질을 분석함
- 몬테카를로 방법
- 난수를 여러 개 발생시켜 시뮬레이션해 근사해를 얻는 방법
- MCMC 방법이라는 명칭에 포함됨
- 마르코프 연쇄
- 어떤 상태에서 다른 상태로 변화하는 현상을 확률로 표현한 모형의 일종
12장. 통계분석과 관련된 그 밖의 방법
주성분분석
- 변수의 차원
- 차원 축소 (dimenstion reduction)
- 데이터의 특징을 유지하면서 분석이나 결과 해석에 도움을 줄 수 있도록 변수의 수를 줄이는 것
- 변수의 수를 줄이는 이유
- 통계 분석에서 변수의 수가 많으면 일어나기 쉬운 다양한 문제들
- 고차원 데이터 해석의 어려움
- 차원을 축소해 2개의 합성 변수로 변환 가능하다면, 2차원 평면에 플롯 그림으로 시각화할 수 있어 해석이 쉬워짐
- 다중회귀분석에서는 설명변수끼리 강한 상관이 있는 상황을 다중공선성이 있다고 하며, 회귀 계수 추정이 불안정해지는 문제가 발생함
- 상관이 있는 변수가 없어지도록 차원축소한 뒤 다중 회귀분석을 수행해야 다중공선성 문제를 피할 수 있음
- 차원의 저주
- 표본크기 n이 충분하지 않은 상황이라면, 회귀계수를 올바르게 추정할 수 없는 문제가 생김
- 고차원 데이터 해석의 어려움
- 통계 분석에서 변수의 수가 많으면 일어나기 쉬운 다양한 문제들
- 차원 축소 (dimenstion reduction)
- 주성분분석 (PCA, Principal Component Analysis)
- 차원 축소에 사용하는 가장 기본적인 방법
- 상관이 있는 변수끼리는 하나로 정리될 수 있다는 아이디어에 기반을 둠
- 새로운 축을 설정하고, 그 축 위의 값으로 데이터를 새롭게 바라봄
- 새로운 축 : 데이터 퍼짐이 가장 커지는 방향으로 설정
- PC1 (제1주성분)
- 가장 새로운 축
- PC2
- 두번째 축
- PC1과 수직 방향이고 데이터 퍼짐이 가장 커지는 방향으로 설정함
- 두번째 축
- 기여율
- 각 주성분이 가진 정보(분산)의 비율
- 누적기여율
- '제1부터 제k주성분까지 전체 정보의 몇%가 포함되는지'
- PC1 (제1주성분)
- 새로운 축 : 데이터 퍼짐이 가장 커지는 방향으로 설정
- 주성분분석 결과
- PC2 이후는 그때까지 얻은 주성분과 직교하도록 설정
- 주성분들이 구해지면, 각 주성분의 기여율과 누적기여율을 확인
- 각 주성분의 값과 원래 각 변수의 상관관계를 계산
- 이를 주성분부하량 또는 인자부하량이라 함
- 원래 데이터를 새로운 변수를 이용하여 표로 나타냄
- 이를 주성분 점수라 함
비지도 학습
정답 데이터가 없으며, 데이터의 배후에 있는 구조를 올바르게 추출하려는 목적으로 사용됨
- 군집분석 (cluster analysis)
- 각 데이터가 어떤 군집에 속하는지를 구하는 방법
- k-means
- 계층적 군집화
- 각 데이터가 어떤 군집에 속하는지를 구하는 방법
지도 학습
- 반응변수 y의 데이터 형태에 따라
- 회귀
- y가 양적 변수일 때
- 분류 (classification)
- y가 질적 변수 (범주형 변수) 일 때
- 이진 클래스 분류, 다중 클래스 분류
- y가 질적 변수 (범주형 변수) 일 때
- 회귀
- 예측과 교차검증
- 지도 학습은 예측에 특화되어 있음
- 예측
- 동일 조건에서 얻을 수 있는 미지의 데이터에 대해 설명변수 x로 반응변수 y를 예측하는 것
- 교차검증(cross validation)
- k-fold 교차검증
- leave-one-out 교차검증
- 이하 생략
- 예측
- 지도 학습은 예측에 특화되어 있음
13장. 모형
수리 모형 : 미분 방정식
- 미분방정식과 차분 방정식
- 대표적인 수리 모형, 결정론 모형
- 미분 방정식 (차분 방정식)
- 시간에 따라 변화하는 변수 x와 시간에 따라 변화하지 않는 파라미터로 구성
- 수리 모형의 목적은 주어진 규칙을 따랐을 때 무엇이 일어나는가 조사
- 시간과 함께 변수 x가 어떻게 변하는가와 같은 시계열 움직임을 대상으로 함
- 미분 방정식 (차분 방정식)
- 대표적인 수리 모형, 결정론 모형
- 수리 모형 사례 : 수의 변화를 모형으로
- 지수함수 증가
- 생물의 개체 수 변화나 감염자 수 변화를 나타낼 수 있음
- 지수 증식의 일반해와 분기 다이어그램
- r=1일 때 시간이 흘러도 x는 변하지 않고 r이 1보다 작다면 지수적으로 감소
- 밀도 효과
- x가 늘어날수록 그 증가율이 줄어드는 효과
- 흔히 로지스틱 방정식이 사용됨
- 지수함수 증가
수리 모형 : 확률 모형
- 무작위 행보 (random walk)
- 1차원 무작위 행보
- 예시) 도박사가 100만원을 가지고 승패 확률이 같은 도박을 시작했을 때, 100 만원은 시간이 지날수록 어떻게 변화할지 표현한 것
- 확률 과정 (stochastic process)
- 확률적으로 시간 변동하는 현상을 기술하는 수리 모형
- 1차원 무작위 행보
- 마르코프 과정
- 무작위 행보를 일반화한 확률 과정
- 과거 상태와는 상관없이, 현재 상태에 따라 다음 상태가 결정되는 확률 과정
느낀점 & 배운점
- 사실 스터디를 위해 더욱 자세하게 정리하고, 그냥 읽으면 증발될 것 같아 요약을 했으나, 요약을 하고도 제대로 이해되지 않는 부분들이 있어 아직 배울 것들이 무궁무진하다는 것을 깨달을 수 있었다.
- 인과추론을 위한 데이터 과학을 수강하면서 배운 다양한 인과, 상관관계의 개념들을 통계라는 거시적인 틀에서 바라볼 수 있어서 좋았다. 다 한 번씩은 배우고 들어본 것들이지만, 막상 남에게 설명하라고 하면 잘 못할 것 같은데, 이 글의 저자는 쉬운 예시를 들어가며 자세하게 설명하고 있다. 나도 어떠한 것을 쉽게 설명할 수 있는 능력을 닮고 싶다는 생각을 했다.
- 며칠 뒤 데이터 분석가 스터디에서 자세히 이에 대한 현업의 얘기를 나눌 수 있으면 좋겠다.
References
책, 통계 101 x 데이터 분석 , 아베 마사토 저, 프리렉
[통계] 모수 (Parameter)와 통계량 (Statistic)을 나타내는 기호 (그리스 문자, 영어 알파벳)
[통계] 모수 (Parameter)와 통계량 (Statistic)을 나타내는 기호 (그리스 문자, 영어 알파벳)
모수와 통계량을 표현하는 문자에 대해 알아봅시다.
jiwondh.github.io
마지막 인사
혹시 이 인사를 보신다면... 분량을 보시면 아시겠지만... 정말 많은 시간과 피땀눈물이 담겨 있습니다...!!
조금이라도 도움이 되셨다면 ❤️를 눌러주시면 감사하겠습니다.
글쓰기를 지속하는 데에 큰 도움과 데이터가 됩니다 :)
감사합니다.
'스터디,책,강의 리뷰' 카테고리의 다른 글
| 글또 8기 데이터 빌리지 반상회 회고 및 후기 (0) | 2023.06.29 |
|---|---|
| "너는 DA니까,알아서 잘 할거야"라는 말을 듣는 사람들을 위한 PM을 위한 데이터 리터러시(프로덕트 데이터 분석) 리뷰 (11) | 2023.06.07 |
| Donebyus (던바이어스) 영어 회화 커뮤니티 2개월 리뷰 (0) | 2023.01.21 |
| 데이터리안 SQL 데이터 분석 캠프 실전반 수강 후기 (5) | 2022.06.11 |
블로그의 정보
다람
darami